本文共 1628 字,大约阅读时间需要 5 分钟。
title: 斯坦福-随机图模型-week1.4
tags: note notebook: 6- 英文课程-9-Probabilistic Graphical Models 1: Representation ---斯坦福-随机图模型-week1.4
独立性 preliminaries 初步
独立的数学描述
对于事建 a, b 如果是独立的那么使用如下的符号进行描述
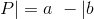
独立的事件有以下的性质:
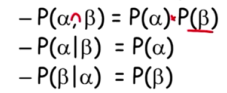
对于随机变量有相似的表示
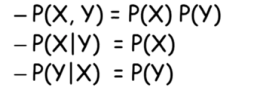
一个例子
还是用之前的成绩问题作为例子:
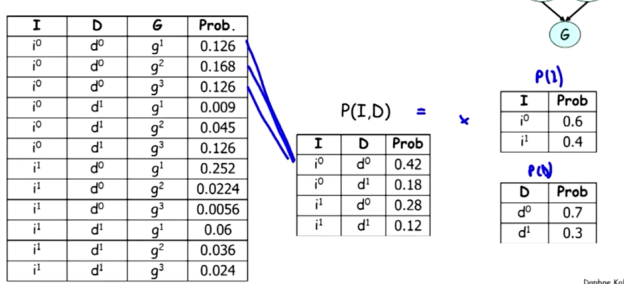
我们可以看到P(I,D)的矩阵中,i0,d0是0.42,正好是P(i0)于P(d0)的乘积,这说明两个变量有可能是独立的。
条件独立
对于有三个随机变量的情况,可以定义条件独立,可以描述为
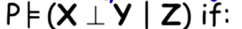
这个条件表述,在Z条件下,x,y是独立的
条件概率有如下的性质
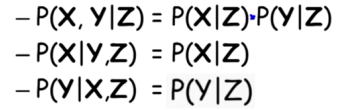
也就是事建X和事件Z的条件下发生Y同事发生的概率等于 Z的条件下发生Y 乘以 Z的条件下发生Y
条件独立的例子
如果你选取一个硬币并且投掷他,假设你不知道者个硬币是什么样的,如果你第一次得到的是正面,那么你对这个硬币的得到正面的概率的估计是什么样的呢?他应该会变得更高。因为你的观测证明他向上的,而你不知道这个硬币是不是均匀的,所以你会倾向于认为这个硬币更容易得到正面。
所以说下次投掷同样得到正面的概率会增加。如果我告诉你,我们的硬币是平均的,那么我们说这两次的投掷就会变得独立,这就是条件独立的例子。贝叶斯网络
独立和分解
根据我们上面的解释,我们讨论了两种独立的现象,他们分别是独立和条件独立:
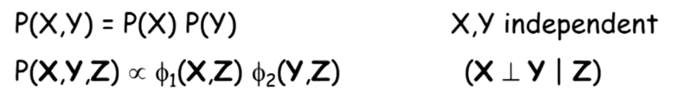
可以看到两种独立性都意味着一种因式分解的可能,我们可以根据这种性质将逗号式拆开,变成乘法式。
提出问题:如果我们的公式p可以写成因式分解的形式,那么是不是说明 G的结构式独立的呢?
影响的流动和 d-separation d分离
定义: 如果在G(Z)中是D分离的,那么在Z的X和Y中没有active trail(活跃的轨迹)
我们可以使用D分离的理论对独立性进行证明。
定理:如果P可以因式分解G,并且在G上有X,Y是D分离的,那么我们认为有X,Y在Z上是条件独立的。
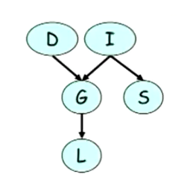
比如我们可以证明在上述图中的D和s是相互独立的:
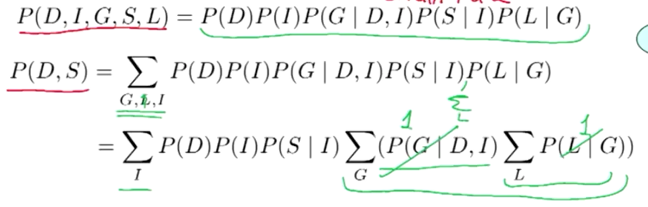
证明的过程是这样的,我们先写出P(D,S)是多少。我们就可以进行因式分解,从而得到:独立的证明式。
D-Separation是一种用来判断变量是否条件独立的图形化方法。相比于非图形化方法,D-Separation更加直观,且计算简单。对于一个DAG(有向无环图)E,D-Separation方法可以快速的判断出两个节点之间是否是条件独立的。
对于较为复杂的DAG图,我们可以给出一个普遍意义上的结论,也就是D-Seperation。对于DAG图E,如果A,B,C是三个集合(可以是单独的节点或者是节点的集合),为了判断A和B是否是C条件独立的,我们考虑E中所有A和B之间的无向路径。对于其中的一条路径,如果她满足以下两个条件中的任意一条,则称这条路径是阻塞(block)的: (1)路径中存在某个节点X是head-to-tial或者tail-to-tail节点(情况一和情况二),并且X是包含在C中的; (2)路径中存在某个节点X是head-to-head节点(情况三),并且X或X的儿子是不包含在C中的; 如果A,B间所有的路径都是阻塞的,那么A,B就是关于C条件独立的;否则,A,B不是关于C条件独立的。I-maps 无关图,
如果在G图中是d分离的,那么P就会符合条件独立的陈述。
我们就可以使用Imap的形式对整个的图像进行描述。
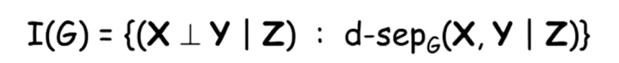
如果我们发现对于所有的P都是条件无关的我们说,P是一个无关图。
比如对于下面的图中:
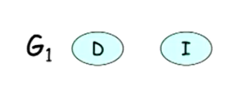
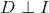
有了上述的基础我们就可以对我们的因式分解的过程进行解释了,我们刚才只是在使用这个公式,并没有有效的证明他,大家可以看到下面的这一部分。
转载地址:http://ezmpa.baihongyu.com/